【解説】2022 鹿児島大学 数学 [2-1]
✓今回の記事
鹿児島大学 数学 教育学部 数学[2-1]を解説します
個別指導で講師をしている
私が解説します
私が解説します
問題はこちらからどうぞ
(1)
方針
logの定義との関係を考える
解答
\( \log_a b = p \)かつ\( a \neq 1 \)とする
\( a^p = b \) となる
これらに対して\( \mathrm{c} \)を底とする対数を取る
$$ \log_c a^p = \log_c b $$
$$ p \log_c a = \log_c b $$
\( \mathrm{a} \neq 1 \) より \( \log_c a \neq 0 \)
したがって
$$ p = \frac{ \log_c b}{ \log_ c a} $$
$$ \log_a b = \frac{ \log_c b}{ \log_ c a} $$
(2)
方針
(1)を使って文字を代入できる形を作る
解答
(1)より
$$ \log_{30} 600 = \frac{ \log_{10} 600}{ \log_{10} 30} $$
$$ = \frac{ \log_{10} {2 \times 3 \times 10 \times 10}}{ \log_{10} 3 \times 10} $$
$$ = \frac{ \log_{10} 2 + \log_{10} 3 + \log_{10} 10 + \log_{10} 10}{\log_{10} 3 + \log_{10} 10} $$
文字を代入する
$$ = \frac{ s + t + 1 + 1}{ t + 1} $$
$$ = \underline{ \frac{ s + t + 2}{ t + 1 }} $$
(3)
方針
置き換えをして考える。その際、定義域に注意する!
解答
$$ y = 2( \log_5 x )^2 – \log_5 x^8 + 6 $$
$$ (1 \leq x \leq 125 ) $$
$$ = 2( \log_5 x )^2 – 8 \log_5 x + 6 $$
\( \log_5 x \) を\(t\)とする
\( 1 \leq x \leq 125 \)より \( 0 \leq t \leq 3 \)となる
$$ y = 2t^2 – 8t + 6 $$
$$ y = 2( t^2 – 4t ) + 6 $$
$$ y = 2(t – 2)^2 -2 \cdot 2^2 + 6 $$
$$ y = 2(t – 2)^2 -2 $$
\( t = 2 \) で軸になる。
\( 0 \leq t \leq 3 \) より
\( t = 2 \)で最小値をとり、 \( t = 0 \)で最大値をとる
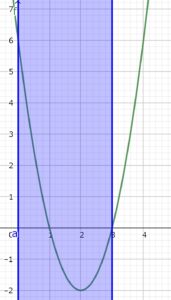
\( t = 2 \) のとき
\( 2 = \log_5 x \)になるので
\( x = 25 \)
\( y \)は頂点なので\( \mathrm{-2}\)をとる
\(t = 0 \)のとき
\( 0 = \log_5 x \)になるので
\( x = 1 \)
\( y \)については\(t = 0 \)を代入すると
$$ y = 2\cdot 0^2 -8\cdot 0 + 6 $$
$$ y = 6 $$
したがって
\( x = 25 \)のとき最小値 \( \mathrm{-2} \)
\( x = 1 \)のとき最大値 \( \mathrm{6} \)
まとめ
きっちり復習をしましょう!(対数、二次関数)
(最後までご覧いただきありがとうございました)
