【解説】2022 鹿児島大学 教育学部 数学 [2-2]
✓今回の記事
鹿児島大学 数学 教育学部 数学[2-2]を解説します
個別指導で講師をしている
私が解説します
私が解説します
問題はこちらからどうぞ
(1)
方針
関数の外の点を通る接線を求める
接することから立式する
接することから立式する
解答
\(y =\sqrt x \) より
$$ y’ = \frac{1}{2 \sqrt{x}} $$
接点を\( (t, \sqrt{t}) \)とすると
接線は\( y = \frac{1}{2\sqrt{t}}(x – t) +\sqrt{t} \)になる
\( (0,1) \) を通るので
$$ 1 = \frac{1}{2\sqrt{t}}(0 – t) +\sqrt{t} $$
$$ 1 = -\frac{1}{2 \sqrt{t}}t + \sqrt{t} $$
$$ 1 = – \frac{1}{2}\sqrt{t} + \sqrt{t} $$
$$ 1 = \frac{1}{2}\sqrt{t} $$
$$ 2 = \sqrt{t} $$
$$ t = 4 $$
これを上の式に代入すると求める接線は
$$ y = \frac{1}{2\sqrt{4}} ( x -4 ) + \sqrt{4} $$
$$ = \frac{1}{4} ( x – 4) +2 $$
$$ = \frac{1}{4} x – 1 + 2 $$
$$ \underline{y = \frac{1}{4}x + 1} $$
(2)
方針
法線と接線の関係から接点を考える。
(接線と法線の傾きの積は-1になることを使う)
(接線と法線の傾きの積は-1になることを使う)
解答
\( \mathrm{n} \)の傾きが\(-2\)なので\( \mathrm{n}\)と\( \mathrm{C}\) が交わる点の
接線の傾きは\( \frac{1}{2} \)になる
これより
$$ \frac{1}{2 \sqrt{x}} = \frac{1}{2} $$
$$ \frac{1}{\sqrt{x}} = 1 $$
$$ x= 1$$
\( \mathrm{C} \)の方程式に代入すると接点は
\( ( 1,1 ) \) になる
傾きが\(-2\)で\( ( 1,1 ) \) を通る直線の方程式は
$$ y = -2( x – 1) + 1 $$
$$ = -2x + 2 + 1 $$
$$ \underline{y = -2x + 3} $$
(3)
方針
グラフを書いてどこを求めるか考える
解答
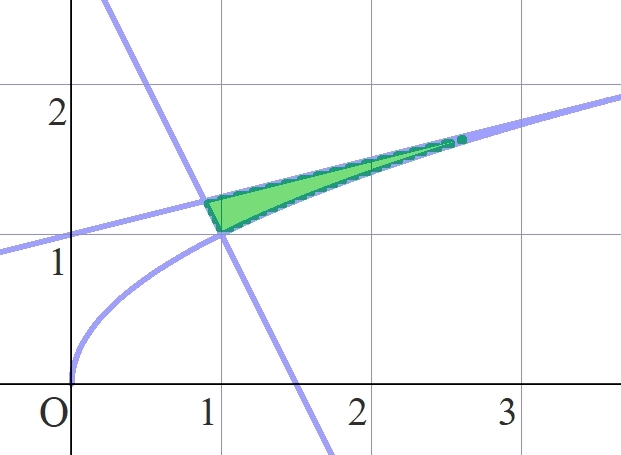
グラフより\( y= \frac{1}{4}x + 1\)の下の部分
\( y = -2x + 3 , y = \sqrt{x} \) の上の部分になる
\(l,n \)の交点は
$$ -2 x + 3 = \frac{1}{4} x + 1 $$
$$ 2 = (\frac{1}{4} + 2) x $$
$$ 2 = \frac{9}{4} x $$
$$ x = \frac{8}{9} $$
よって求める面積は
$$ \int_{ \frac{8}{9}} ^{1} (\frac{1}{4} x +1 – (-2x + 3)) dx $$
$$ + \int_{1} ^{4} ( \frac{1}{4} x + 1 -( \sqrt{x} ) ) dx $$
$$ = \int_{ \frac{8}{9}} ^{1} ( \frac{9}{4} x-2) dx $$
$$ + \int_{1} ^{4} ( \frac{1}{4} x + 1 -x^{\frac{1}{2}} ) dx $$
$$= \left[ \frac{9}{8} x^2 – 2x \right]_{\frac{8}{9}} ^{1} $$
$$ + \left[ \frac{1}{8}x^2 + x -\frac{2}{3} x^{ \frac{3}{2}} \right]_{1} ^{4} $$
$$ = \frac{9}{8} 1^2 – \frac{9}{8}( \frac{8}{9})^2 – 2( 1 – \frac{8}{9} ) $$
$$ + \frac{1}{8}(4^2 -1) +4 – 1 – \frac{2}{3}(4^{ \frac{3}{2}} -1^{\frac{3}{2}}) $$
$$ = \frac{9}{8} – \frac{8}{9} – \frac{2}{9} + \frac{15}{8} + 3 – \frac{14}{3} $$
$$ = \frac{24}{8} – \frac{10}{9} + 3 – \frac{14}{3} $$
$$ = 6 – \frac{10}{9} -\frac{42}{9} $$
$$ = 6 – \frac{52}{9} $$
$$ \underline{ \frac{2}{9}} $$
まとめ
きっちり復習をしましょう!(微分、積分)
(最後までご覧いただきありがとうございました)
